Article Sidebar

PDF
Date Published: 27/06/2021
Online Published: 28/06/2021
Abstract Views: 173
Views PDF: 121
DOI: https://doi.org/10.54607/hcmue.js.18.6.3071(2021)
Issue
Vol. 18 No. 6 (2021)
Section
Natural Sciences and Technology
How to Cite
Lê , V. C. (2021). SUBGROUPS OF THE UNIT GROUPS OF A GROUP ALGEBRA. HCMUE Journal of Science, 18(6), 1064. https://doi.org/10.54607/hcmue.js.18.6.3071(2021)

SUBGROUPS OF THE UNIT GROUPS OF A GROUP ALGEBRA

Văn Chua Lê

Main Article Content

Abstract

 

Let G be a group and F a field. A subgroup H of the unit group (FG)* of the group algebra FG is said to be almost subnormal if there exists a sequence of subgroups

 

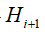
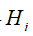
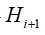
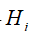
such that for any 0<=i<r either  is normal in  or  has the finite index in  In this paper, we show that if G is a finite nilpotent group, F is a pythagorean field, F admits only archimedean orderings, and every quaternion division algebra A over F is isomorphic to the ordinary quaternion algebra  then almost every subnormal subgroup of the unit group (FG)* of the group algebra  is normal in(FG)*

 

Keywords

almost subnormal subgroup, group algebra, pythagorean field

Article Details

References

Casolo, C., & Mainardis, M. (2001). Groups in which every subgroup is f-subnormal. J. Group Theory, 4, 341-365.
Golubchik, I. Z., & Mikhalev, A. V. (1982). Generalized group identities in the classical groups. Zap. Nauch. Semin. Lomi An SSSR, 114, 96-119.
Greenfield, G. R. (1978). A note on subnormal subgroups of division algebras. Can. J. Math, 30, 161-163.
Hartley, B. (1989). Free groups in normal subgroups of unit groups and arithmetic groups. Contemp. Math, 93, 173-177.
Hazrat, R., & Wadsworth, A. R. (2009). On maximal subgroups of the multiplicative group of a division algebra. J. Algebra, 322, 2528-2543.
Le, V. C. (2019). Nhom con cua nhom nhan trong vanh chia quaternion thuc [Subgroups of the multiplicative group of the division ring of real quaternions]. Ho Chi Minh City University of Education Journal of Science, 12(16), 975-981.
Mahmoudi, M. G. (2020). On normal subgroups of the unit group of a quaternion algebra over a pythagorean field. Bull. Iran. Math. Soc, 46, 253-262.
Nguyen, K. N., Mai, H. B., & Bui, X. H. (2017). Free subgroups in almost subnormal subgroups of general skew linear groups. Algebra i Analiz, 28(5), 220-235, English translation in St. Petersburg Math. J., 28(5), 707-717.
Roquette, P. (1958). Realisierung yon Darstellungen endlicher nilpotenter Gruppen. Archiv. Math. 9, 241-250.
Tomanov, G. M. (1985). Generalized group identities in linear groups. Math. USSR, Sbornik, 51, 33-46.
Trinh, T. D., Mai, H. B., & Bui, X. H. (2020). On division subrings normalized by almost subnormal subgroups in division rings. Periodica Mathematica Hungarica, 80, 15-27.
Wehrfritz, B. A. F. (1993). A note on almost subnormal subgroups of linear groups. Proc. Am. Math. Soc, 117(1), 17-21.